Cet article fait partie d’une série d’articles sur le machine learning. Je vous conseille d’aller lire mon premier article consacré au perceptron si vous ne l’avez pas déjà fait.
Dans l’article précédent, je vous ai présenté l’élément de base des réseaux de neurones, le perceptron. Nous avons vu, au travers d’un exemple, comment résoudre un problème linéaire à l’aide de celui-ci.
Mais on se retrouve vite avec des problèmes non linéaires qui ne peuvent pas être résolu par un seul perceptron.
L’opération booléenne basique : le XOR ou « Ou exclusif » est un exemple très simple qui illustre bien le problème. Pour rappel, cette opération retourne « vrai » uniquement si une seule des deux valeurs est vraie.
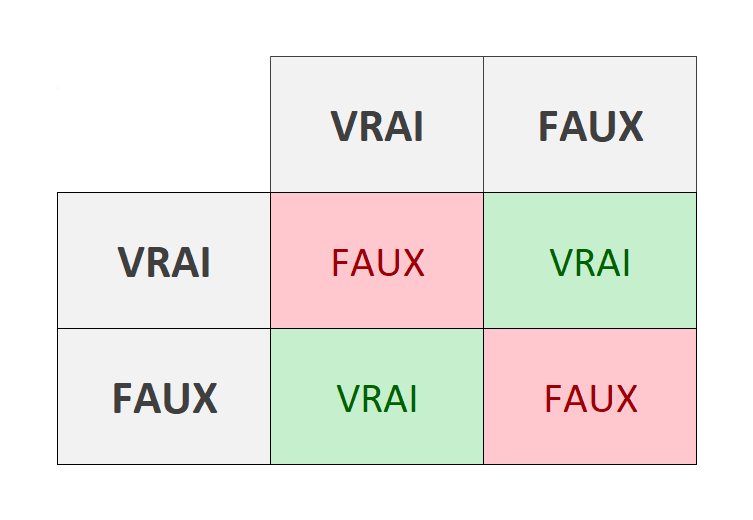
Ce problème n’est pas linéaire. Pour vulgariser, si l’on prend le tableau ci-dessus, vous ne pouvez pas tracer une ligne droite qui sépare les vrais et faux. Pour résoudre le problème, l’astuce consiste à connecter plusieurs perceptrons entre eux pour former un réseau.
Dans cet article, nous allons voir comment créer ce réseau de neurones à l’aide de notre perceptron.
Algorithme de prédiction
Pour prédire le résultat, nous allons utiliser un algorithme de propagation. Les neurones seront organisés en couche, dont chaque neurone recevra en entrée toutes les valeurs de sortie des neurones de la couche précédente, ce que l’on appelle un perceptron multicouche. (multilayer perceptron)
Dit comme ça, j’imagine que ce n’est pas très clair 😉 Mais pas de panique, je vais vous l’expliquer. Voilà déjà à quoi ressemble un réseau :
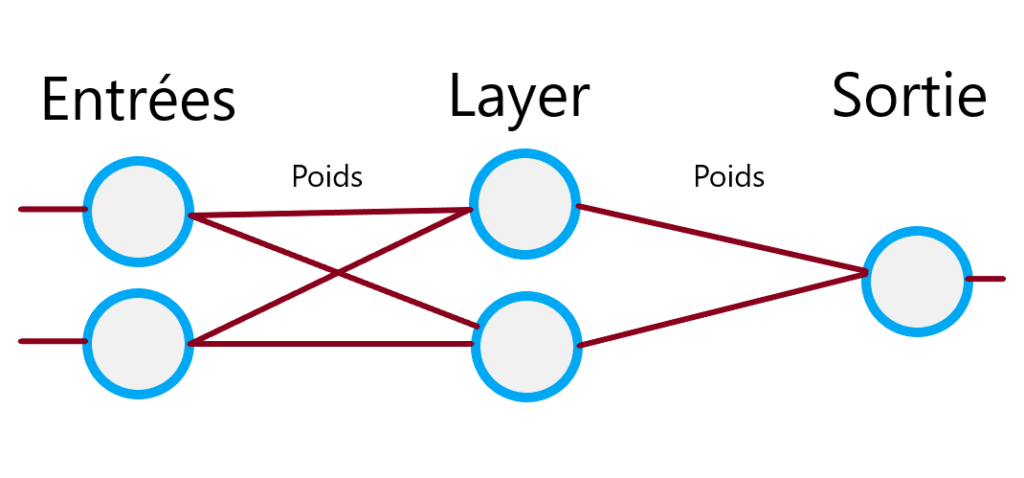
Le réseau est composé de plusieurs colonnes qui correspondent à nos couches. Chacune de ces couches peut avoir un ou plusieurs nœuds, nos perceptrons.
Nous avons tout d’abord la couche d’entrée de notre réseau. Par exemple avec l’opération XOR, nous lui passons deux entrées correspondant à nos valeurs vraies ou fausses.
Viennent ensuite plusieurs couches cachées (hidden layers). Ces couches vont permettre le fonctionnement de notre réseau.
Finalement la couche de sortie, dans laquelle nous recevons le résultat. Avec le XOR, nous attendons qu’un seul résultat, mais il est tout à fait possible d’en recevoir plus.
Comme je vous l’expliquais dans mon dernier article, notre perceptron est une boite qui reçoit plusieurs entrées et retourne une seule sortie. Si l’on isole un perceptron de notre réseau, voilà ce que cela donne.
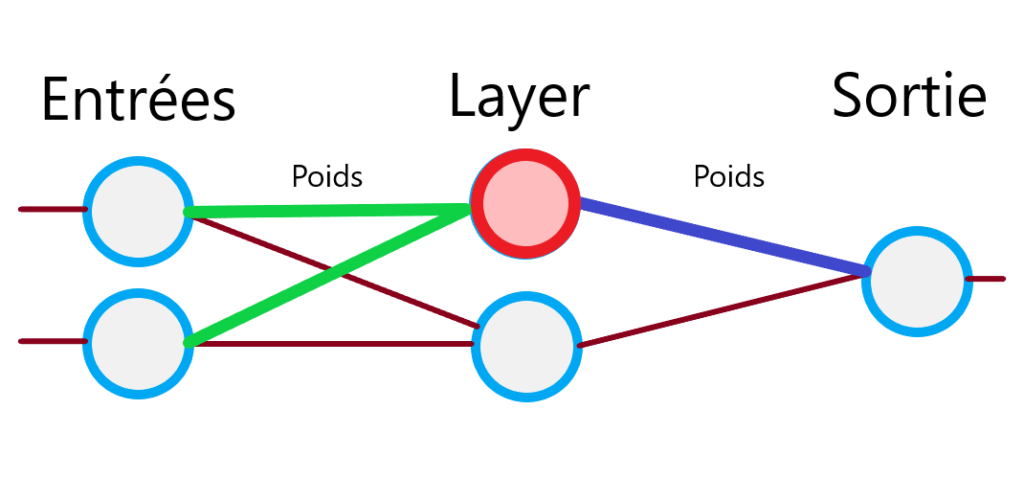
La différence par rapport à l’utilisation d’un perceptron seul, c’est que nous allons utiliser la sortie des précédents comme entrée sur les suivants. Chaque sortie sera envoyée à tous les perceptrons de la couche suivante. Ce sont les poids des sorties qui vont pouvoir être ajustés pour faire évoluer notre réseau de neurones.
Voilà un exemple qui illustre comment les valeurs sont propagées à travers le réseau :
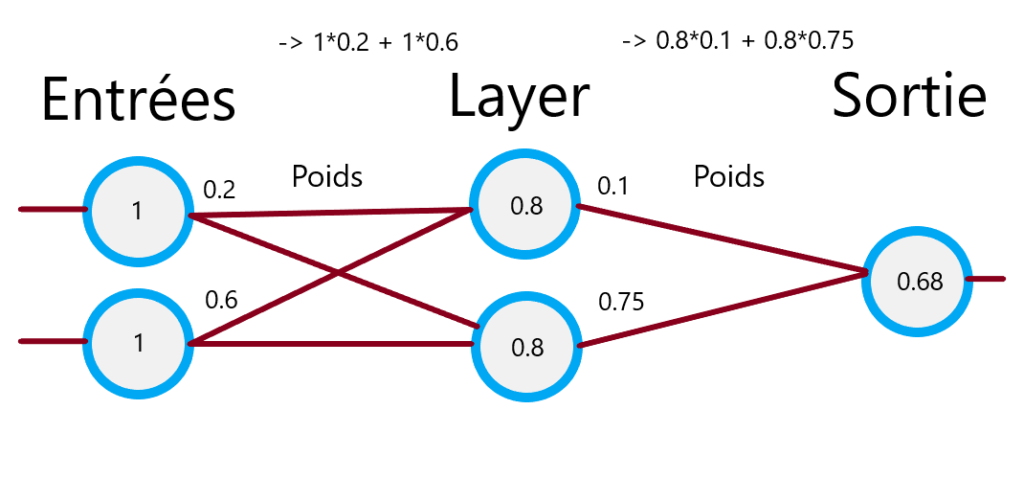
Apprentissage et rétropropagation
L’intérêt derrière ce système est de pouvoir l’entrainer pour qu’il apprenne à résoudre un problème. Pour cela, nous allons avoir besoin d’un jeu de données dont nous connaissons le résultat.
Dans le cas du XOR, voilà les données que nous connaissons :
var inputs = [
[[0,0], [0]],
[[0,1], [1]],
[[1,0], [1]],
[[1,1], [0]]
]Le système est similaire qu’avec un seul perceptron, nous allons calculer la marge d’erreur par rapport au résultat attendu. La correction est propagée depuis la sortie vers les couches précédentes et permet d’adapter la valeur des différents poids.
Exemple dans Godot
Pour illustrer le fonctionnement, j’ai créé un projet sur Godot Engine avec un réseau de neurones. Le programme va tenter de résoudre l’opération XOR que nous avons vue plus haut.
Les quatre coins correspondent aux valeurs de nos opérations booléennes ([0,0], [0,1], etc.). Je génère ensuite une grille en nuance de gris qui va nous montrer l’évolution du réseau.

Les coins vont petit à petit converger vers les valeurs attendue (noir pour 1 et blanc pour 0).
Vous trouverez toutes les sources de ce projet sur Github. N’hésitez pas à tester le code par vous même.
La suite
Dans mon prochain article consacré aux réseaux de neurones, nous verrons une autre méthode d’apprentissage : la neuroévolution. Cette méthode s’inspire du principe de l’évolution et est très pratique quand nous ne connaissons pas les données à l’avance.
Jusque-là, je vous ai montré des problèmes très basiques, la prochaine fois je vous montrerai un exemple plus ludique avec des voitures qui apprennent à conduire sur un circuit.

